Решение задач с параметрами в GeoGebra
- Использование среды GeoGebra при решении задач с параметрами
Ниже ссылка на методическую разработку и сама задача
Пожалуйста, не забудьте правильно оформить цитату:
Уханова, Л. В. Использование среды GeoGebra при решении задач с параметрами / Л. В. Уханова. — Текст : непосредственный // Школьная педагогика. — 2018. — № 3 (13). — С. 40-44. — URL: https://moluch.ru/th/2/archive/104/3512/ (дата обращения: 11.01.2023).
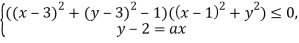
Задача: Найти все значения параметра a, при каждом из которых система: не имеет решений. Решение: В первом неравенстве дано произведение двух выражений. Первое из них описывает окружность с центром в точке (3;3) и радиусом 1, а второе — точку (1;0). Т. к. само неравенство меньше нуля, то его решением будет объединение внутренней части окружности и точки. Уравнение в системе — это семейство прямых: . Для того, чтобы данная система не имела решений необходимо отсутствие пересечения прямой с окружностью, а также прохождения через точку. Выполним построения в компьютерной среде GeoGebra и найдем значения параметра, при которых данная ситуация будет выполняться.
Я лишь попробовал визуализировать процесс нахождения решения в системе ГеоГебра,
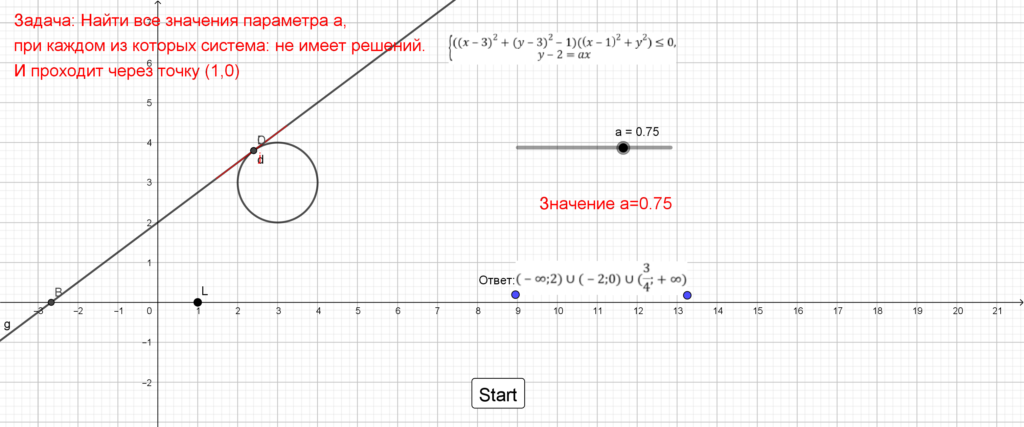
При нажатии на кнопку Start начинается анимация ползунка а, задающего параметр в прямой. В точках касания этой прямой с окружностью происходит сравнение координаты точки касания прямой и координаты точки касания отрезка касательной к окружности, построенной дополнительно. При совпадении значений анимация приостанавливается и выводится сообщение значения параметра а в этот момент.
Мои попытки сделать то же самое при пересечении прямой и точки L оказались неудачными. Шла остановка чуть раньше значения -2.
Сложнее всего скорее интерпретировать результаты, т.к. речь идёт о нахождении отсутствия решения.
Ссылка на исходный материал https://moluch.ru/th/2/archive/104/3512/
Ссылка на файл ГеоГебра https://disk.yandex.ru/d/6YAsbrISs3ihMg